One of the most common tasks done with lines is detecting their intersection. For some reason, not many people know how to do that on a computer. In this post, I assume you have some lines. You got them from some algorithm, or the user supplied them, or whatever. And you want to find the intersection of these lines.

Step 1: Converting lines to Ax + By = C

Ideally, the lines should be in the form Ax + By = C. But usually, that is not the case. But it is simple enough to convert it into this form. This is done using the two point form of the line.

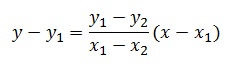
We can generate two points on the line using the given form, And then plug those points into the above equation. And thus you'll get the equation in the form we want.

Rearranging the two-point equation, we get: (just try and understand them... they're not as horrible as they seem :P)

On opening the brackets on the right hand, we get:

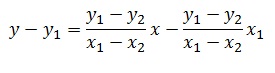
And multiplying by (x₁-x₂) and rearranging, we get:

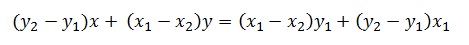
Compare this to Ax + By = C... and you'll see that we have our equation!

• A = y₂ - y₁
• B = x₁ - x₂
• C = By₁ + Ax₁

So, convert all your lines into this form, and we're ready for step 2. Actually figuring out intersection points.

Step 2: Solving for intersection

Right now, we have several lines in the form Ax + By = C. So "solving for intersection" is just solving a set of equations:

A₁x + B₁y = C₁ A₂x + B₂y = C₂

To solve, multiply the first equation with B₂ and the second with B₁. Then you end up with:

A₁B₂x + B₁B₂y = B₂C₁ A₂B₁x + B₁B₂y = B₁C₂

Subtract the second equation from the first and you get:

A₁B₂x - A₂B₁x = B₂C_{1 -} B₁C₂

And thus, we get the x coordinate of intersection:

x = (B₂C_{1 -} B₁C₂) / det

Where det = A₁B₂ - A₂B₁

Similarly, you can derive an equation for y. And finally, we arrive at these results:

• x = (B₂C₁ - B₁C₂) / det
• y = (A₁C₂ - A₂C₁) / det

If det = 0, then the lines are parallel (so you cannot calculate x and y)

Conclusion

Translate the equations in bullet lists into a program. And you have a program that solves for intersection of lines!